Earthquakes caused by dams
Title: Earthquakes caused by dams
Author: R. Ashok Kumar
Corresponding(first) author: R. Ashok Kumar
Mailing Address: 1/13, Telec Officers’ CHS., Ltd., Plot 30, Sector 17, Vashi, Navi Mumbai- 400703
Phone: 022-27896209
E-mail address: rakumra@yahoo.com
Copyright ©2017 Ramaswami Ashok Kumar
AUTHOR'S NOTE FOR VIEWING IMAGES
To view blackened images, please right click on the image and put on a separate tab, then right click on the image in the new tab(expand if necessary) and click on image info to view the table. Author
Invocation
https://m.youtube.com/watch?v=qQxlNZzdggI&list=RDMM31vQFHBhJoQ&index=4
Prelude
Mother Earth of Nature
Man part of nature!
With democratic powers
Shocking and awesome
Full of greedy thoughts
Conquering nature
Amassed special wealth
There is false knowledge
Clinging to one as if it
Were all heedless of
The consequences
Heedless of the harm to earth
Narrow dull and dark
Destroying marshes
Killing mangroves and swamps
Old trees on hillsides
Subcontinent cleared!
Reservoirs great were built fast
They rapidly filled
During all monsoons
And rapidly were they drained
Every dry season
Dams year after year
Dotted the subcontinent
Countlessly increased
On inter(intra) faults
Water moments changed so fast
They quaked mother earth
Dams controlled earthquakes!
Till at last great ones occurred
So shallow off land
Boomeranged back west
Fast accurate tsunamis!
Creating chaos!
Men part of nature
Destroying nature for self
Themselves sure destroyed!
They are the culprits
They should relearn harmony
Specialists modern
Reforest the earth!
Reverdure your call before
More great boomerangs!
Demolish excess!
Life way born out of nature
Womb of mother earth!
Is forever safe
Healthy wholesome longlasting
You part of nature!
R. Ashok Kumar
Earthquakes caused by dams
By R. Ashok Kumar, 1/13, Telec Officers’ CHS., Ltd., Plot 30, Sector-17, Vashi, Navi Mumbai- 400703. E-mail: rakumra@yahoo.com
Date of article July 2005
The paper examines the consequences of harnessing rainfall behind some 4500 dams in India. Changes of geological magnitude are occurring in an instant, rivaling the effects of ‘tectonic plate forces’. The article provides epidemiological evidence including correlation with stress relief in rocks to show that the force and moment waves, because of dams on the Indian subcontinent are a cause of the waves of worldwide earthquakes. Dry season earthquake parameters in percent are a faithful reproduction of those for the monsoon. A significant race is on between the two seasons to record the biggest earthquake ever. The paper expects earthquakes of magnitude 8 MM or greater in the coming monsoons following the displacements caused by the 9.4 MM great Andaman earthquake. The article shows that the pendulum of the earthquake wave has synchronized with the pendulum of the wave of applied rate of change of water moment-a state of chaos.
Key words: hydro- cycle, India, dams, force surges, moment-surges,waves of earthquakes, causality, displacements, prediction, chaos.
INTRODUCTION
The earthquake at Bhuj on 26th January 2001 was preceded and followed by a number of earthquakes worldwide. The pattern depicted by this phenomenon raised a question whether the archimedian lever effect caused by the oscillating weight of waters behind large dams on the Indian subcontinent caused earthquakes worldwide. The earthquakes were so far thought to be caused by some dams only locally by the pore pressure effect. However, the dynamics of the earth appeared to be affected by the rapidly rising concentration of waters behind dams during the gigantic transfer of rain-waters from the oceans to the Indian subcontinent by the South-West monsoon and by the withdrawal of the waters during the dry season thereafter. Hence the following hypothesis was formulated and investigated.
THE HYPOTHESIS
In this article a hypothesis is proposed that the weight of waters behind dams on the Indian subcontinent exerts rapidly changing moments on faults, which display stick-slip behavior. This results in earthquakes worldwide with a regularity typical of the South-West monsoon on the Indian subcontinent, followed by water withdrawal during the dry season. The hypothesis is tested by a statistical analysis of earthquake data and its correlation with water moments caused by dams. Dams other than the Indian are excluded from the study. The reasons are as follows. Assuming that the study shows a statistically significant result that the dams in India are causing worldwide earthquakes, there
are two possibilities for the result for a study with the other dams excluding 1)the Indian dams and 2) other dams in areas having similar hydrological cycle: Either the result is significant, in which case the others act similar to the Indian, or the result is not significant, in which case the other dams do not cause worldwide earthquakes.
THE WATER MOMENT AND ITS RATE OF CHANGE
The 124 year rainfall data (1871-1994)(Columbia University Website) for each month from June to September, was used to compute the mean rainfall and the running mean rainfall for each of these months for India and expressed in percent of the running mean rainfall total for June to September. The monthly rainfall is taken as a measure of the change in the water moment during the month. The weight of water acting at the center of gravity of all the water masses behind the reservoirs exerts moments in all directions about the center of gravity. This moment becomes effective whenever a fulcrum is offered at the faults (stick-slip phenomenon). The dry season period from October to June witnesses water withdrawal from the reservoirs and is assumed to be a linear draw down from 100 percent storage at the begin of October to zero percent storage by the end of May. It is not the water moment, but its rapid rate of change that is being studied here for its effects. Today simultaneously, behind dams in India part of the Indian subcontinent more than 300 billion cubic meters (BCM) of water are collected each year during the monsoon. The dam storages rise from zero at the commencement of the monsoon to more than 300-400 BCM in just 4 months. This is withdrawn in 8 months of the dry season from October to May. Thus at the center of gravity (23,78.75) of these water masses, a gigantic surge wave of the rapidly changing vertical load rises from zero to 300-400 billion tons in 4 months of monsoon and slumps to zero by end May. This is a force application at the center of gravity of the water masses whose wave rises at the rate of about 326 million newtons per second during the monsoon. This is a giant wave of changing load at the rate of 33000 tons per second or equivalent to a rapidly rising water column head of 33 kilometers per square meter every second at the center of gravity for 4 months of the monsoon: a pressure wave of 325 million pascals per second! During the dry season from October to May, this reduces progressively to zero by release of a wave of force at half this rate! This caused a total rate of change of water moment on the Sagaing fault during the 2000-2001 hydrological year of the order of 1183*10^19.05 Nm/year(Table 7). This corresponds to a surge wave of bending moment at the Sagaing fault, changing at the rate of 420 million megawatts (MW) of power during the whole year! Note that during four months of the monsoon, one half of the total annual change of water moment of 1183*10^19.05 Nm was applied on the Sagaing fault, which is a rate of change of applied bending moment of 630 million megawatts power. During the dry season of eight months, the remaining half of the change in bending moment was released at half this rate or 315 million MW. During the same year the total seismic moment released during 1-9.9 MM (moment magnitude) earthquakes in the region, -90 to 90 degrees latitude and 78.75 to 180 degrees longitude, was 987 *10^19.05 Nm. This is an average seismic moment release at 351 million MW of power! So we are dealing with geological time scale and type variations in an instant (every second of every year). Such gigantic waves of repeated alternating rate of change of moment applications throughout the year, every year, on faults, and their consequences, form the subject matter of this article. With deep continental roots and cratons welded to the underlying mantle (Pratt 2000), it is possible indeed that the force and moment surge waves travel throughout the earth and when they meet faults, the stresses build up causing them to snap releasing earthquakes.
THE SCIENCE OF THE INVESTIGATIONS
The method used has followed those of science: The principle of the canon of agreement: same antecedents: the worldwide earthquakes following from dams which harness the common factor: the rains; conditions of difference: dams and no dams: effects and no effects; independent laws: a number of favourable instances from the worldwide earthquake data base confirm truth of the hypothesis linking cause to effect and effect to cause. The plausibility: for instance same ratio seismic moment to change of water moment as the stress relief ratio in rocks; dry season and monsoon outcomes of earthquake patterns are reproductions of one another and related rigidly to reservoir content changes.
A study of the USGS database on worldwide earthquakes (USGS WEBSITE) in the range 1-9.9 MM brings out the following findings:
Dam Era
Highly significant correlation of percentage values of earthquake parameters with percentage change of water moment.
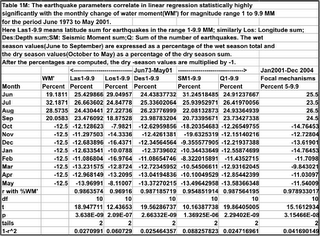
The monsoon and dry season earthquake parameters latitude, longitude, depth, seismic moment and the number of earthquakes summed up each for each month, cumulatively for each year, and expressed in percent of the wet and dry season sums respectively, display statistically highly to extremely significant linear regression, when correlated with the corresponding monthly percent change of water moment (Table 1).
In Table 1, the dry season values in percent are multiplied by -1 to get Table 1M.
Table 1M shows that the correlations are all statistically extremely significant. This is because when water is drained off the dams, the change in water moment is opposite in direction to that when the dams are filling up(and hence the seismic moments become negative). To see the corresponding changes in the other earthquake parameters we multiply their respective percent dry-season values also by -1. This process then shows up the correlations around the water moment changes during the dry season.
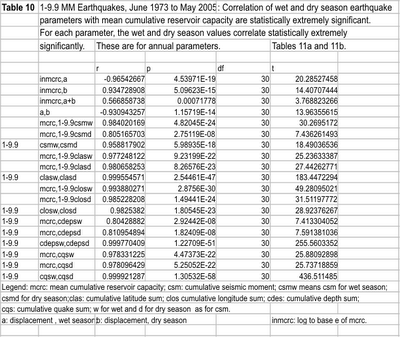
The linear regressions for each year correlate with the yearly cumulative reservoir capacities in a logarithmic regression.
The trajectory of the Linear Regression correlation r (%WM’, %y, an earthquake parameter) of the cumulative monthly sums of the earthquake parameters with the annual cumulative reservoir capacity (June 1973-May 1974,June 1973-May 1975,…June 1973-May2001) for the various earthquake parameters is shown in Figure 1: This regression is logarithmic and is statistically extremely significant (Table 2). The reservoir capacity (RC) (and water storage) is given in million hectares created irrigation potential equivalent (Mha CIPE). The reservoir capacity in billion cubic meters(BCM) is got by multiplying the reservoir capacity expressed in million hectares created irrigation potential equivalent (Mha CIPE) by the factor (water application at canal head in meters/efficiency of water storage).
The F-Ratio Test on the Earthquake Parameters and the Rate of Change of Water Moment
The F-Ratio Test for the variables %WM’ and the earthquake parameters of Table 1 shows that they all come from the same parent population (Table 3). The F-Ratio Test provides further evidence that the rate of change of water moment and hence the dam storage variations govern the earthquakes persistently. Here sdp is the standard deviation of the population, p(F) is the probability of the F-Ratio being exceeded by chance and df is the number of degrees of freedom. The F-Ratio probability shows that the percentage rate of change of water moment and the various earthquake parameters in percentage are statistically not significantly different.
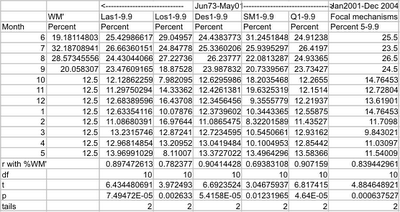
Percent Focal Mechanisms per month correlate with Percent Rate of Change of Water Moment: January 2001 to December 2004
This connection of earthquake parameters to rate of change of water moment was tested by correlating available data on beachball representations (focal mechanisms) with the monthly rates of change of water moment(Table 1). Those, which exhibited tension at the top end of the beachball representation, were counted for each month for each hydrological year. The mean count for each month was expressed as a percentage of sum of such means for the two seasons respectively. When the percent mean counts were correlated with the percent rates of change of mean water moment in linear regression, it was found that the foci exhibit a statistically extremely significant correlation: r=0.839,p= 0.000638. Further, the chi-square distribution is 7.38 with p=0.77,degrees of freedom 11, showing that the differences between the two quantities are due to chance. Thus the stresses in the rocks appear to be controlled by the rate of change of water moment.
Predam Era and Transition to the Dam Era
A similar study for the predam era –2150 to 1850 and transition to the dam era till 1951 shows no such statistically significant correlation (Focal mechanism data was not studied as data was not available for this period). See Table 4. The data for significant worldwide earthquakes (5.5-9.9 MM) of the USGS data base from 2150 BC to 2001 AD was used. It was assumed that the monsoon rain magnitudes expressed in percent of the total for the monsoon remain invariant statistically whatever era is being considered in the period being studied. The monthly change of water moment is still given by the monthly rainfall, but the effect is governed by the rainfall that is harnessed by collecting the waters behind dams as surface water storage.
The Relation of Seismic Moment to Water Moment
Dam Era
Four statistically extremely significant results were deduced on the basis of scaling procedures developed below.
First Result
For the 1973-2001 database when the annual rate of change of water moment is compared with the annual seismic moment sum for all earthquakes in the 5.5 –9.9 MM and in the range 1-9.9 MM, it is found that the annual cumulative mean of the ratio of the seismic moment sum to the corresponding change of water moment to be statistically the same as the stress relief ratio for rocks, that is, stress relieved from rocks during earthquakes as a percentage of the stress built up in the rock prior to earthquakes(19.743%)(Turcotte and Schubert, 2002) (Table 5,Figures 2,3,4 and Table 7, Figure 5).This connects the stress build up in the rocks at the faults to the waves of force on account of the dams.
Second Result
The ratio of the yearly seismic moment sums on either side of the center of gravity of the water masses converges to the corresponding ratio of the initiating water moment arms (Figures 4, 6, Table 7). This identifies and quantifies the effect of the water moment waves.
Third Result
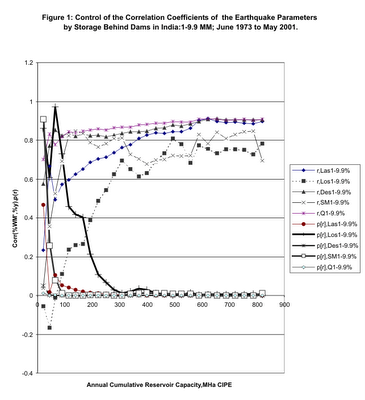
For the earthquake range 1-9.9 MM, it is found that the mean latitude per quake and 90- mean longitude per quake for the period June 1973 to May 2001 are not significantly different from the location of the center of gravity of the water masses (23,78.75)(Figure 7). This confirms the relation of the worldwide earthquakes to the cause- the giant force waves at the center of gravity. The longitude of the mean hypocenter has to be different from that of the center of gravity, to produce the wave of water moment changes to cause the wave of earthquakes (Table 8). In Table 8, the computations use the straight line connecting the center of gravity to the mean annual hypocenter for the water moment arm and arrive at the same result as the compuation method of Table 7(which is as described under scaling procedure below). The latter uses the initiating water moment arms, which for 1-9.9 MM quakes are the lines connecting the center of gravity to the Sagaing fault on the right and to the Murray Ridge on the left of the center of gravity. The extremely close correlation(Table 1) with percent change of water moment, shown by both the student’s t test and the chi square distribution, of the latitude sum, the depth sum and the sum of earthquakes within the hydrological year spanning the period June 1973 to May 2001 also significantly show the dams as a cause of the worldwide earthquakes.
Fourth Result. The worldwide earthquake pattern for the Indian dry season is a reproduction of that for the Indian monsoon and vice versa.
During the monsoon reservoir build up the force at the center of gravity of the water masses exerts moment at faults resulting in stress build up leading to earthquakes by the stick- slip phenomenon. During dry season water release from the dams causes forces to act at the faults in the opposite direction to that during the monsoon causing earthquakes. And consequent displacements occur in a direction opposite to that in the monsoon. This is the hypothesis in case the dams do cause worldwide earthquakes. Partitioning the data into monsoon and dry season sets and analysis shows that the displacements for the two periods are a mirror reflection of one another and cancel out leaving a comparatively small but significant net displacement per earthquake. Adding the data for the monsoon and the dry seasons separately for each year cumulatively filters out transients and brings out the persistent cause and the hypothesis is proved right : Referring to Table 9, the monthly displacements are related logarithmically to the mean reservoir content buildup and discharge(buildup: r = -0.964, p = 0.036; discharge: r = 0.9305, p = 0.0007967). The other earthquake parameters in this table have similar statistically extremely significant logarithmic relations with the mean reservoir content (Figure 8). The correlations between displacements and the other earthquake parameters of Table 9 are linear and statistically extremely significant. The correlations between the annual mean cumulative reservoir capacity and the annual values of earthquake parameters are also statistically extremely significant as Table 10 shows which is derived from Tables 11a and 11b. Figure 9 shows the chi-square analysis for displacements, which confirms the mirror reflection. The rapid build up behind dams cause one set of injuries to the living earth by earthquakes whose displacements are sought to be negated by another set of earthquakes during the dry season of water use, causing another set of injuries. For a particular season, beginning from a particular hydrological year, as shown in Table 11, the cumulative displacement from all the earthquakes is computed as the cumulative seismic moment sum till a particular year per mean applied force at the center of gravity of the dams till that year. This is then divided by the cumulative number of quakes to arrive at the displacement per quake. The mean applied force in newtons is computed from the mean cumulative reservoir capacity till that year. The net displacement in a year is taken as the sum of the positive displacement per quake in the monsoon and the negative displacement per quake in the dry season. As an example, the net displacement till May 2001 from June 1973 was 0.7 m/Q for the year of the Bhuj 8.0 MM quake on 26th January 2001, while it was –24.4 m/Q till 9th May 2005, in the year of the great earthquake of 9.4 MM in the Andaman Basin on 26th December 2004. In Figure 9, the great Andaman quake was taken as of 9.0 MM. If it is considered a 9.4 MM quake, we neglect this huge value, and consider for the chi-square sum, values till 2003, to see the persistent dam effect. Because of the persistent surges of bending moment and force applied on faults, the great Andaman quake may well have been triggered by the dams in India. On the basis of the mirror reflection hypothesis growing out of this evidence, a series of strong to huge earthquakes should occur in the coming monsoon(s) as a reaction to the huge negative displacement deficit for the dry season ending 31 May 2005. The surge of release of water from all dams in the dry season reproduce effectively the earthquake pattern of the monsoon, when the reservoirs contents rapidly build up synchronously and vice versa.
Study of peak magnitudes for reflection of wet season performance in dry season and vice versa.
Table 12 reveals this reflection of one season’s performance in the other by means of the dry season- monsoon season race to register the maximum unprecedented earthquake, driven rigidly by the waves of reservoir content changes: The 1974 and 1975 dry seasons register 8.1 MM and 8.2 MM maximum magnitude earthquakes. The wet season of 1976 replies with 8.0 MM quake. The 1976 dry season registers an 8.1 MM quake. The 1977 and 1978 monsoons record 8 MM each. The monsoons of 1979,1980 and 1985 record 8.1, 8 and 8.1 MM quakes respectively. The 1986 and 1988 dry seasons reply with a record 8.3 MM quake and an 8.2 MM quake. The 1993 and 1994 monsoons register unprecedented wet season highs of 8.2 MM each. 1994 dry season replies with 8.3 MM. The 1995 monsoon registers 8 MM for the maximum magnitude quake for that year. The dry season of 1995 registers 8.2 while that of 1997 and 1998 register 8.3 each. The 2000 monsoon then replies with an all time high of 8.3 but the dry season of 2000 answers with 8.2. The monsoon of 2001 soars to a record unprecedented 8.4 MM maximum magnitude quake. The 2001 dry season replies with 8.0 but that of 2002 has an unprecedented record of 8.5! The 2003 monsoon registers 8.3. Then the 2004 dry season replied with an all time high of 9.4 MM. And already North Chile recorded in the monsoon season, on 13th June 2005, a major quake of 7.9 MM. The correlation between the cumulative reservoir capacity and the moment magnitudes in Table 12 is high(r=0.5452,p=0.0048,degrees of freedom 23), pointing to the fact that the regression of the race is statistically very significant.
THE DAMS CONTROL WHEN EARTHQUAKES OCCUR
The dams determine the timing of the earthquakes rigidly as shown in Figure 11 for the period June 1973 to May 2005. The mean duration of the peak magnitude earthquake for each month correlates statistically extremely significantly with the corresponding monthly mean change of water moment, with all values expressed as percentages of the respective seasonal totals :Linear regression: r=0.9, p= 6.24E-05; X^2= 7.34; p= 0.77. The yearly running mean of the mean of each of the seasonal durations separately also exhibit statistically extremely significant correlations with the relentlessly increasing cumulative dam storage capacities(logarithmic correlation)(Figure 12)(r(wet)= -0.9286; p= 1.87E-14(June 1973 to May 2005); r(dry)= -0.9322; p= 1.56E-12(June 1978- May 2005).
See http://glaringlacuna.blogspot.com/
Predam era and the transition to the dam era
For the predam era and the transition to the dam era no such laws were found (Table 13).
Further as we pass from the predam era to the dam era, the number of major and great earthquakes in the longitude band 0-180 degrees more than doubles statistically extremely significantly compared to that in the longitude band 0 to -180(Table SDMGQ). A more detailed evaluation confirms the significant doubling of the relative risk(Table MGOPNL). Together with the fact that the Indian dams are situated in the 0- 180 longitude band and the other results deduced in this paper, this doubling of the relative risk is indeed caused by the Indian dams. For evidence on the exponential rise of the number of Indian dams in the 20th century see Figure 0.



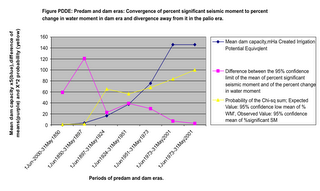
WATER MOMENT CONTROLS SEISMIC MOMENT IN DAM ERA
The 95 percent confidence limits of the percent significant seismic moments(observed values) converge to the corresponding limits of the percent change in water moment(expected values) in the dam era. But they diverge away from the expected values in the predam era(Table 4a and Figure PDDE).The chi-squared distribution probability for the chi-squared sum for the pre-dam era and the dam era shows extremely significant difference in the two means for the predam era and no significant difference in the two means during the dam era. In Figure PDDE, the last point on the chi-squared probability curve is shown as 100% and is the upper limit of the expectation. When we consider the negative signs for the values of the water moments in the dry season and the corresponding percent seismic moment values negative, the chi-square probabilities for the dam era become 96.5% percent while those for the pre-dam era become 0.1 percent. The conclusion therefore remains the same, that, together with the other results of this article, this evidence shows that the persistent surge waves of earthquakes worldwide during every hydrological cycle are being persistently caused by Indian dams. The detailed analysis of the pre-dam era and the dam era is contained in Table CSMWM(ignoring dry season negative signs) and Tables PDERA and DERA (with negative signs for the dry season values considered).
Confirmation of Causality of India Dams Causing Worldwide Earthquakes
A study of All-India daily rainfall and Worldwide daily earthquake response confirms that the risk of daily worldwide earthquakes as measured by Seismic Moment per unit daily All-India Rain is not significant in the pre-dam era, while it is significant in the dam era. Further, during the dam era, the significance of the correlation of the risk on a daily basis depends on the strength of the July rains.
See
http://worldwidedailyearthquakerisk.blogspot.com/
This result unequivocally confirms that Worldwide earthquakes are being caused by Indian dams.
The scaling procedure
The nature of the initiating water moments: On what faults are the water moments initially exerted? The significance of the mean value of the earthquake parameter.
On account of the control exerted by the rate of change of water moment on the earthquake parameters, the mean hypocenter for a quake in any year as given by the latitude per quake, the longitude per quake and the depth per quake(determined as the sum of the values of the parameter under consideration divided by the number of earthquakes during the period) is used to derive values for the initiating or earthquake triggering water moment arms. On a two dimensional fractured surface map of the world(Cartographic Division, National Geographic Society, 1995) (Figure 2), the mean location for a quake in any given year is plotted and joined by a straight line to the center of gravity (CG) (23,78.75), of the water masses behind dams in India (See Appendix A for the derivation of the location of the center of gravity). This line is then extended upwards to meet the Himalayan Frontal Thrust (HFT) fault line in the north. In the south the line crosses the Owen Fractured Zone (OFZ) or the Carlsberg Ridge (CR) or the Mid- Indian Ridge (MIR). The two water-moment arms are then 1) CG-HFT and 2)CG-OFZ or CG-CR or CG-MIR. The total water moment arm for computation of the total rate of change of water moment is then HFT-OFZ or HFT –CR or HFT-MIR. These statements hold good for earthquakes in the range 5.5-9.9 MM during the period June 1973-May 2001. It is noteworthy that for this period of the study, the limits as shown in Figure 2 for these lines are a narrow band and they all intersect the Himalayan Frontal Thrust north of the center of gravity, CG and either of the three faults as mentioned above, south of it.
The initiating water moments from the scaling procedure.
Table 5 displays the data for earthquakes in the range 5.5 to 9.9 MM for the years 1973-74 to 2000-01. It shows how the water moments are computed which are acting on the faults which exhibit a stick- slip behaviour resulting in earthquakes due to these water moments. This should be referred to in connection with Figure 2, which illustrates the situation created by the water moments and their changes due to the monsoon and the dry season. During the monsoon the reservoirs fill up increasing the bending stresses on the stick- slip faults resulting in earthquakes when the faults snap. During the dry season when water is being withdrawn for use, these moments are released resulting in stress relief and again consequent earthquake occurrence. A similar situation exists for the earthquakes in the range 1-9.9 MM resulting in ratios statistically indistinguishable to those for 5.5-9.9 MM quakes (Figure 3).
Computation of the rate of change of water moment for any year for worldwide earthquakes.
Let us first take the earthquakes in the range 5.5 to 9.9 MM. Let us take the year 1973(See Table 5). Corresponding to the location, [(mean latitude, Las/Q, mean longitude, Los/Q)]=(4.27108, 60.7636), a line is drawn on a two dimensional fractured surface map, connecting this mean epicenter to the center of gravity, CG, of the water masses (23,78.75). This straight line passes through a point say MIR, on the Mid Indian Ridge below the centre of gravity, CG and meets the Himalayan Frontal Thrust fault, at say HFT, north of the CG. On the map (scale 1 inch=758 miles at the equator), these arms of the water moment CG-MIR and CG-HFT measure 6.7 cm and 2.1 cm respectively. The total of the two water moment arms (CG-MIR+CG-HFT) is 8.8 cm (called the total water moment arm and denoted by WMAT). The water moment arm above CG (above 23o N latitude), CG-HFT, is called WMA>23,for the arm meeting the Himalayan Frontal Thrust. This is entered in the column captioned WMA>23 and the value for the year 1973 is 2.1. The next column is the worldwide sum of the seismic moments in the range 5.5 to 9.9 MM for each year; for 1973, the value is 223.1*10^19.05 N-m. For all earthquakes worldwide occurring in latitudes>23o N latitude, the seismic moments in the range 5.5 to 9.9 MM are summed up and entered in the column marked SM>23. The value for 1973 is 90.6*10^19.05 N-m. The total rate of change of water moment for any year in Newton-meters is given by twice the product of the weight of water masses behind dams (in newtons) and the sum of the water moment arms north and south of the centre of gravity(CG) of the water masses in meters. This is because at the end of the monsoon the rate of change of water moment as measured by the total rainfall is a maximum equal to the total reservoir capacity in India. During the dry season, October to May, this water is withdrawn for use, till the reservoirs are empty by the end of May. So the total rate of change of water moment during the dry season, October to June, is measured by the total water storage available at the end of the monsoon. This is also the total reservoir capacity because of the shortage of water on the Indian subcontinent. For comparing the effect of water storage capacities from year to year, however, the effective water moment arm from the centre of gravity of the water masses to the concerned fault must be factored in. The total rate of change of water moment in newton-meters/year for worldwide earthquakes for latitudes greater than lat, WM’>lat, and corresponding water moment arm, WMA>lat, for any year, is given by
WM’>lat=2*RC (Mha CIPE*)[10^10 m^2]*(Water application at canal head,0.8m/Storage efficiency,0.8)(m)[m^3][10^3kg]*9.81(msec^2)[N]*WMA>lat(cm)/2.54(in)*758(miles)*1.58(km)*[10^3m]N-m/year (1)
=9251.0617328*10^16*RC*WMA>lat N-m/year (2)
=(9251.0617328*10^16/10^19.05)*RC*WMA>lat *10^19.05 N-m/year (3)
=8.245017448*RC*WMA>lat *10^19.05 N-m/year (4)
Thus, for worldwide earthquakes for all latitudes and longitudes, if the total rate of change of water moment for any year is denoted by WM’T and total water moment arm is WMAT, then
WM’T= 8.245017448*RC*WMAT *10^19.05 N-m/year (5)
And for worldwide earthquakes for latitudes >23 degrees,
WM’>23=8.245017448*RC*WMA>23 *10^19.05 N-m/year (6)
For the year 1973, RC is 20.7 Mha, WMAT=8.8 cm and WMA>23 is 2.1 cm; WM’T, from Equation (5) works out to 1502 *10^19.05 N-m and WM’>23, from Equation (6), becomes 358.41*10^19.05 N-m.
An assumption is made for the reservoir efficiency of 0.8 and for the water application at canal head of 0.8m, for the purposes of this study. Still with Table 5, for 1973, ratio SMT/WM’T*100= 223.1/1502*100= 14.853%. And SM>23/WM’>23*100=90.6/358.41*100=25.291%. The various ratios of the seismic moment to rate of change of water moment are entered in Table 5 as T%, meaning SMT/WM’T%; >23% meaning the ratio SM>23/WM’>23%; the cumulative mean of the ratio SMT/WM’T% is CM T%; the cumulative mean of SM>23/WM’>23% is entered in the column CM>23%. The moment magnitude range of the earthquakes for which these ratio values are entered are indicated in the respective columns as either just 5.5-9.9 or just 1-9.9. The captions O1, O2 for the cumulative ratios indicate that those ratios are used as observed values in computing the chi-squared sums; similarly the caption E indicates that the ratio is the expected value in determining the chi-square values.
Analysis of Correlation of Earthquakes in the Range 1-9.9 MM with Rate of Change of Water Moment
The water moment arms for each year hit the Sagaing fault to the right of the center of gravity (23,78.75) and pass through the Murray Ridge to the left. The water moment arms, like for the 5.5-9.9 MM earthquakes, form a narrow cone on either side of the center of gravity. There is a clockwise shift in the cone by about 30 degrees from 5.5-9.9 MM epicenter line to the 1-9.9 MM epicenter line connecting the center of gravity (Figure 2,Table 7, Figure 5).
Dance of the Earthquakes in Synchronism with the Hydrological Cycle becomes tighter with more dams commissioned on the Indian SUBCONTINENT: CHAOS.
With each annual hydrological cycle, the annual feature of the earth’s response to the oscillatory rate of change of water moment is cyclically repeated. See the hold on the earthquake parameters exercised by the rapidly increasing storages in the monsoon behind Indian dams and the occurrence of the earthquakes during the dry season when the water moments applied on the faults are released as the waters are drained from the dams (Figures 10-10b). The control becomes stronger as more and more dams are commissioned on the subcontinent of India as revealed by the closer correlation displayed by the earthquake parameters (Figure 1). Table 2 shows the logarithmic regression between the storages and the correlation between the percent seismic moment and percent change in water moment is r=0.710, 26 degrees of freedom with probability of the two-tailed t-distribution 2.2868E-05(June1973- May2001). The hypocenter and the number of quakes also show this attribute. That the control by the dams is plausible is also seen by the specific nature of the correlations connecting to the ground realities. The latitude mean for the earthquakes is that of the center of gravity, the location of which is on the earth’s surface. Thus the power of the waves of bending stresses exerted by the dams is maximum at or near the earth’s surface. Hence the 1-9.9 MM, June 1973 to May 2001 earthquakes have a mean depth of 6.57 km!(Tables 11a and b). The longitude can be all round the center of gravity because the moments are exerted all round. But see result 3: the longitude is shown to be constrained to a mean of 90 – the longitude of the center of gravity. This is for the range of reservoir capacities built so far! The nature of the earth is not, however, under the type of rigid control seen statistically, regarding the number of quakes, the latitude and the depth. The earth appears to finally decide on the timing of an earthquake, the longitude and the amount of seismic moment released during an earthquake(Table 12). Even here the control by the dams is indisputably statistically significant. Together with the quantification of the control of worldwide earthquakes with dam storages developed here, this brings out a characteristic feature of the observed phenomenon: Chaos. There is a disturbance pendulum which we recognize here as the rate of change of water moment. And there is a response pendulum -the worldwide earthquakes- characterized by their parameters as discussed above. The response pendulum, year after year, as the dams on the subcontinent increase, merges with the disturbing pendulum. The similarity to the synhronization of feedback responses described in Sarasola et al(2003) is striking(both created by man). The statistical results presented here have established by Student’s t tests, the F-ratio test and Chi square analyses that the synchronization is effectively complete. A giant experiment in chaos has been unwittingly let loose on the earth by the dams by their gigantic waves of force and bending moment changes on faults every year.
Conclusions.
This paper furnishes statistically highly significant whole earth epidemiological evidence that dams in India are also causing worldwide earthquakes in the range 1-9.9 MM. The rates of change of water moment exerted on faults by the water masses behind dams cause shallow earthquakes to occur on account of the well- known stick-slip phenomenon. The ratio of the arms of the water moment on either side of the center of gravity of the water masses controls the ratio of the corresponding seismic moments in a persistent manner recurring with each hydrological cycle: the monsoons and the dry season of water withdrawal: the cumulative mean of the ratio of the annual sum of the seismic moments north of the center of gravity for 5.5-9.9 MM (east of the center of gravity for 1- 9,9 MM) to the total annual sum converges to the mean of the corresponding ratio of the leverage arms of water moment. The monthly rates of change of water moment as measured by the monthly all India rainfall govern the number, location, depth and seismic moment magnitude and timing of the earthquakes occurring worldwide by causing the monthly sums of these parameters to be statistically highly significantly proportional to the corresponding rates of change of water moment(when expressed as percentages of the wet and dry season sums of the respective variables). This robust control of the earthquake parameters allows us the use of a scaling procedure for measuring the total annual rate of change of water moment as a function of the dam storage and the water moment arms. It turns out that the cumulative mean of the ratio of the annual seismic moment sum to the annual rate of change of total water moment converges to the stress relief ratio in rocks persistently with extreme statistical significance. The variations of the cumulative annual sums of the earthquake parameters are practically completely explained by the variations of the corresponding annual cumulative sums of the rapidly changing dam storages. The paper tests these results against the earthquake data for the pre-dam era and the transition to the era when dams exert significant control over earthquakes. There is no significant statistical correlation between water moment changes (monthly rainfall during monsoon and the rate of release of water moment during the dry season) and earthquake parameters in the pre-dam era or the incipient dam era contrasting with the results for the dam era (all values expressed in percentages of the respective seasonal totals). The control over earthquakes by dams each hydrological year becomes stronger as more dams are commissioned in India with consequent increase in the effect of the monthly rains and the total monsoon rains in the same fixed time span (in 4 months of monsoon and 8 months of dry season) manifesting as increasing stress changes in rocks. Dry season earthquake parameters do not differ statistically significantly from the monsoon parameters. The displacements at the faults caused by the dams during the dry season are opposite in direction to those caused by the dams in the monsoon so that the net displacement is a comparatively smaller quantity, though substantial in absolute terms. There is a race between the dry season and the monsoon to establish ever-higher records of peak magnitude earthquakes, with the monsoon always lagging behind, time-wise as well as magnitude-wise. Because of the sudden huge gap of a net negative displacement caused by the great Andaman Basin earthquake of 9.4 MM on 26th December 2004, the coming months would see the reflection of this in the form of a series of strong and huge earthquakes in the monsoon(s) throughout the world. This is a giant global experiment set off by the dams resulting in a chaotic system, whereby the pendulum of the earthquakes synchronizes with the pendulum of the rate of change of water moment. This calls for a fresh approach to the harnessing of rainfall and for a reappraisal of dams.
Acknowledgements
The author thanks adversarial reviewers of an early version of the manuscript for their comments. Also the author wishes to place on record the data base providers for the useful sources referred to in this work.
Appendix A
Centre Of Gravity Of Stored Water Behind Dams
A map of India was taken on a suitable scale , in this case it was 1 inch = 116 miles(National Geographic Society, 1997). The distances of the water bodies from Bhuj were measured and inserted into the equations :
X = Sum(Si* Xi)/Sum Si (1)
Y = Sum (Si *Yi)/Sum Si (2)
Where
Si = Storage of dams in state i, assumed to be located at the center of the state ;
Xi,Yi are the x and y coordinates of the water bodies of state i from the origin taken to be Bhuj arbitrarily, and
X and Y are the coordinates of the centre of gravity of stored water behind all the dams in all the states.
Thus the center of gravity, CG , has latitude and longitude as given by:
Latitude of CG = Latitude of Bhuj + Y (3)
Longitude of CG = Longitude of Bhuj + X (4)
Referring to Table 58(Tata services Ltd., Department of Economics and Statistics, 1999) for the year 1998-99, we read off the total irrigation potential (IP) created up to 1993-94 for Major and Medium dams for the various states(a measure of the dam storages) and enter them into equations 1 and 2 above. We also enter into them the x and y coordinates from the origin- Bhuj, for the water bodies for each state as read off from the map :
We tabulate in the form of a table for convenience (Table A)
Thus the x and y values in equations 1 and 2 above are
x=12.5 and y= -0.6
Thus from equations (3) and (4), with appropriate readings from the map referred to above, the Latitude of CG becomes
Latitude of Bhuj + ‘y’= 23
And the longitude of CG becomes
Longitude of Bhuj + ‘x’ = 78.75
References
Cartographic Division, National Geographic Society, 1995. The Earth’s Fractured Surface. 2D Tectonic Map of the World . National Geographic Magazine. April
Columbia University Website: http://ingrid.Ldgo.columbia.edu/Sources/Indices/.india/.rainfall/
National Geographic Society, 1997. Map: South Asia. National Geographic Magazine. May
Pratt D., 2000. Plate Tectonics: A Paradigm Under Threat. Journal of Scientific Exploration. Vol. 14, pp. 307-352.
Sarasola C., Torrealdea F. J., D’ Anjou A., Moujahid A., Grana M.,. 2003. Feedback
Synchronisation of Chaotic Systems. International Journal of Bifurcation and Chaos, Vol. 13, No.1, 177-191.
Tata Services Ltd. Dept. of Economics and Statistics.1999. 1998-99. Irrigation Potential Created by Large and Medium Sized Projects. Table 58. 1993-94 and for 1996-97. In Statistical Outline of India. Bombay House. Mumbai-400001. For other years the same source for those years. For certain years when data was unavailable, they were extrapolated from available data using compound interest formula.
Turcotte, D.L., and Schubert,G., 2002. Faulting: Earthquakes. In Geodynamics . 2nd Ed.Cambridge University Press.UK. Chap.8. p 353.
US Geological Survey( USGS )Website: http://wwwneic.cr.usgs.gov/neis/epic/epic.html
Tables and Figures follow after the epilogue. To get Table 1 which is showing blacked out, click on the image. You see the Table 1. Alternatively, below this blacked out image is the table 1 without the caption.
EpilogueHomeland Refugees
To Reverdure
Homeland refugees
Whose land is their homeland
Created by selfish concentration
Of rainwater by dams
On the subcontinent Indian
Worldwide seismic moments shallow
By destroyers of forests follow
Driven by magnificent monsoons every year
Damned by Hydroelectricks!
Natural intrinsic control lost
Of equitable water distribution
Replaced single mindedly by surface reservoirs
Relentlessly silted up by the rushing rains
Lake after lake becoming a barren landscape
Welcome homeland refugees to hell
By hydroterrorists, rainwater robbers:
The stupidest peasant or tribal
Is more competent, yes Wendell Berry
Than the most intelligent in a society
Of inhuman specialists!
Ramaswami Ashok Kumar
TABLES AND FIGURES










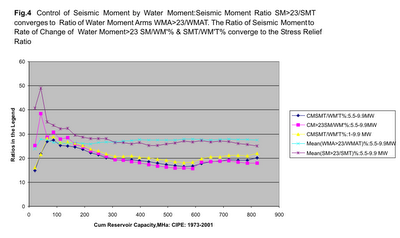

Figure 2: The Initiating Water-Moments. Scale: 1 inch=758 miles














Copyright ©2008 Ramaswami Ashok Kumar







0 Comments:
Post a Comment
<< Home